Legends of Code & Magic - a Codingame contest
Codingame
I now work at Flaneer, feel free to reach out if you are interested!
Codingame is a website where you can solve puzzles, work on optimization problems, and build bots for games. You have access to a vast range of codding languages, and I personally mainly used Java, Python & C++. What I enjoy the most is to build AI for multiplayer games: a card game, a quidditch match, a Tron battle, etc.


Legends of Code & Magic (LOCAM)
The game
This is a game created by Jakub Kowalski and Radosław Miernik, in cooperation with Codingame. This is a card game, opposing two players. The game is turn-based, zero-sum, and without a possibility to tie. It is important to note that you only have 100ms to play each turn. The game is separated into two parts :
- First, you have to draw 30 cards from a pool of 160 cards. During 30 turns, the game will propose you three cards, and you have to choose the one you want to pick.
- After that, each player will play. I can do several actions: summon a creature, attack the opponent, use an item, etc.
- The game will end whenever someone’s hp drop to zero.

The rules
We can split the game into several components: Drawings, Mana, Creatures, and Items.
-
Drawings: The first player starts with four cards, while the opponent begins with five. Each turn you will draw a new one (some of them might even allow you to draw several cards at the same time).
-
Mana: You can only use a card if you have enough mana. Both players start with one Mana and gain one for every turn they play.
-
Creatures: Creatures have a mana cost, attack points, and defense points. Some creatures start with specific abilities. By default, creatures can’t attack the turn they are summoned, and they can attack only once per turn. When a creature attacks another one, they both deal damage equals to their attack to the defense of the other creature. When a creature attacks the opponent, it deals damage equals to its attack to the HP of the opponent.
-
Items: When played, items have an immediate and permanent effect on the board or the players. They can modify the attack or defense of a creature, add or remove abilities. They can also damage or heal the opponent or yourself. You can find three types of items: green items (positive effect on your creatures), red items (harmful effect on the opponent’s creatures) and blue items (effects on yourself or the opponent directly).
As for the six special abilities :

-
Breakthrough: Creatures with Breakthrough can deal extra damage to the opponent when they attack enemy creatures. If their attack is higher than the defending creature’s defense, the excess damage is dealt to the opponent.
-
Charge: Creatures with Charge can attack the turn they are summoned.
-
Ward: Creatures with Ward ignore once the next damage they would receive from any source. The “shield” given by the Ward ability is then lost.
-
Lethal: Creatures with Lethal kill the creatures they deal damage to.
-
Guard: Enemy creatures must attack creatures with Guard first.
-
Drain: Creatures with Drain heal the player of the amount of the damage they deal (when attacking only).
My bot
My bot was split into several parts. The first one was dealing with the Drafting phase. It was a simple heuristic with a score for each card. The second part was dealing with the summoning phase, while the last one dealt with the attacking phase. I built both of them with variants of Monte-Carlo methods and Monte-Carlo Tree Search.
You only have a limited amount of time when you play :
| Actions | Allocated time |
|---|---|
| Response time per turn | 100ms |
| Response time for the first draft turn | 1000ms |
| Response time for the first battle turn | 1000ms |
Monte Carlo
Intuitively, a Monte-Carlo method means that we will use several random draws to approximate the value of something. It could mean: shooting random arrows in a square with a circle in it. The proportion of arrows into the circle will allow us to approximate $\pi$. In a game, we could simulate random moves and evaluate them to find the best sequence of move possible.
On a more mathematical point of view, let $x_1, x_2, …, x_N$ be i.i.d. laws, following the same law as a random variable $X$. For any borelian fuction $f$ (with $f(X) \in L^1$), we can calculate the following approximation :
\[\mathbb{E} (f(X)) = \frac{1}{N} \displaystyle \sum_{i=1}^{N} f(x_i)\]In fact, if we denote $I = \mathbb{E}(f(X))$ and $I_N = \frac{1}{N} \displaystyle \sum_{i=1}^{N} f(x_i)$, we have thanks to the strong law of large number :
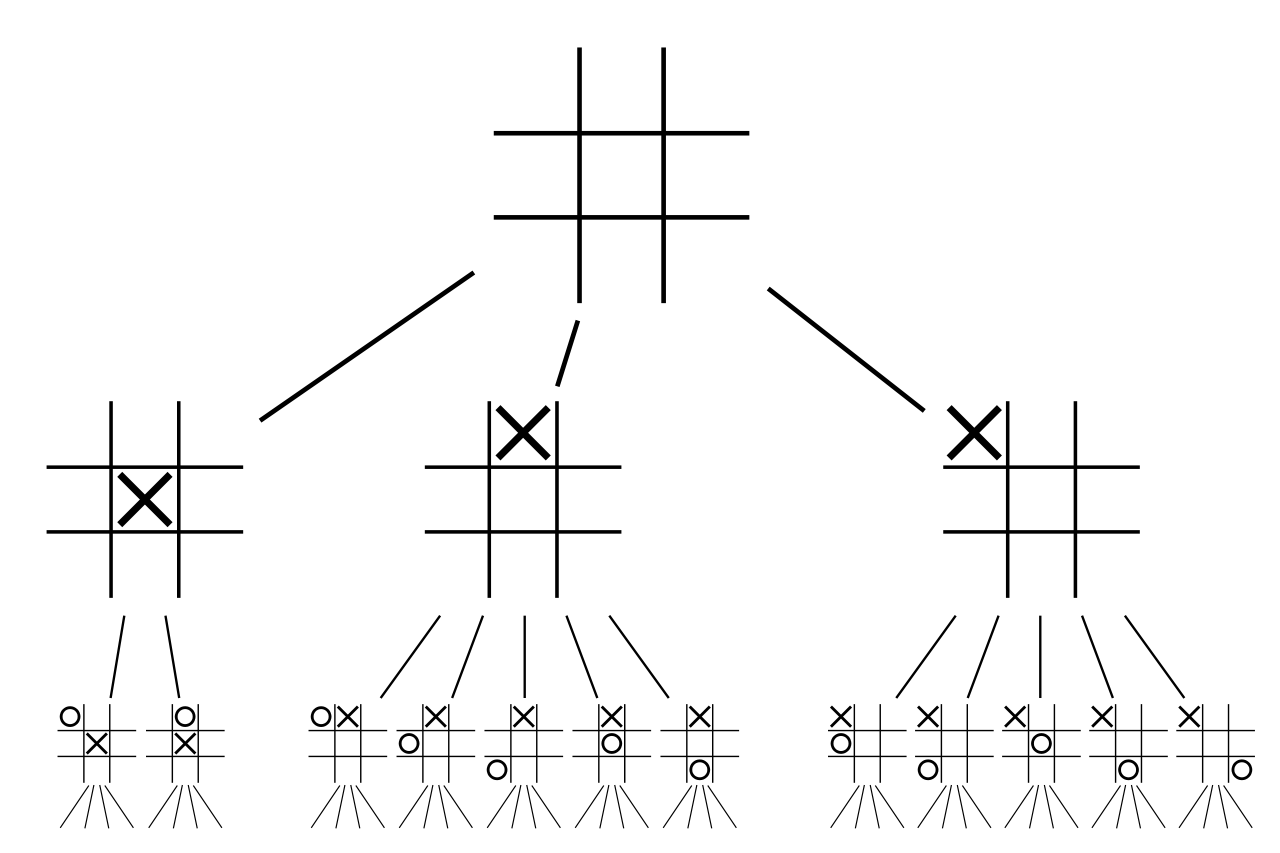
\[I_N \rightarrow I \; \; a.s.\]For example, let’s say we are playing a game of tic-tac-toe. Every time we have to play, one solution could be to perform several random moves, evaluate them (which one is the most promising?) and play the best. Even more, we could also play several sequences of random moves (e.g.,: one move for me - one for my opponent - one for me) and apply the same strategy.
MCTS
Now, a Monte-Carlo method has several flaws, but one of them is the fact the moves are drawn randomly. We could spend a lot of time simulating moves that are not interesting at all. Therefore, an idea would be to simulate and evaluate the more promising moves. This is called a Monte-Carlo Tree Search.
The first idea is to view a game as a tree: each node being one possible state of the game.
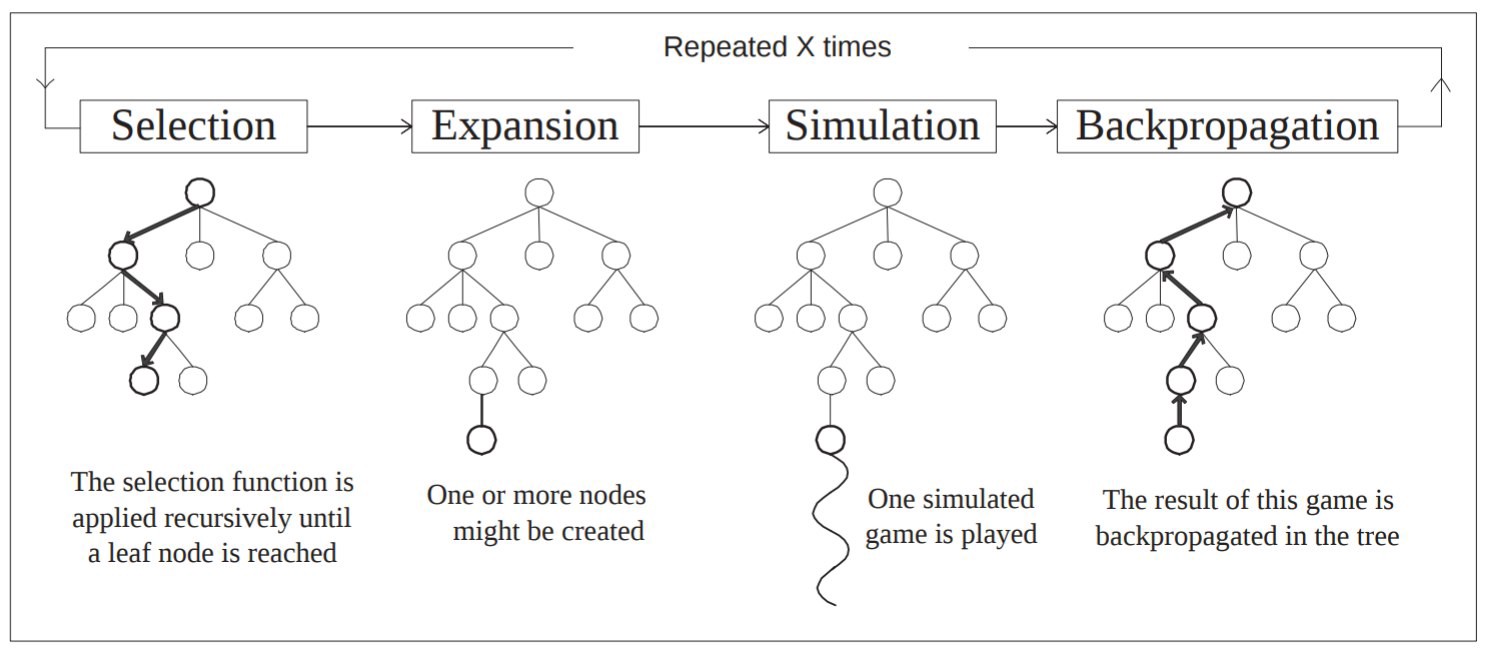
An MCTS always follows the same four steps:
Selection
Starting from the root, we select childrens, often following the UCT formula (the node maximizing the following):
\[\frac{w}{n} + c\sqrt{\frac{\ln{N}}{n}}\]where $w$ is the amount of win from this node, $n$ the amount of time we visited this node, $N$ the amount of time we visited this node’s father and $c$ an exploration parameter. This formula is supposed to give a good comprise between exploration and exploitation.
Expansion
If the selected node isn’t terminal, we simulate one child from it.
Simulation
We simulate a game, starting from this child until we reach a terminal state.
Backpropagation
Since we reached a terminal state, we can update every visited node with the new information: we lost, or we won.
Evaluation function
An MCTS supposes that it is possible (in a reasonable amount of time) to reach a terminal state. Now, this might not be possible: only partial observations (like in this game, where you can’t predict the hand of the opponent), computational time that is too heavy, etc. Therefore, it is interesting to define an evaluation function (like in Evolutianory Algorithm): the goal of such a function is to characterize how good (or bad) a state of the game is.
Draft phase
When the contest started, I believed that the draft phase would not be the crucial part of the contest. As it will turn out, this was a mistake. My first strategy was to follow a mana curve (a sort of gaussian, with a mean at 6 of mana). If this strategy worked fine at first, this was not the best choice.
After some talks with other coders from the contest, the idea of hardcoding a score for each card emerged. The plan would then be to draw the card with the higher score. The real question was: how to compute such scores? The strategy I used was to build genetic algorithms; each individual of the population being a set of scores for each card.
In order to evaluate each individual, I used several methods. All of them are based on the same strategy: playing many games with this draft against another fixed one, and keeping the win rate as the score of the individuals.
In the end, this method gave me a score for each card, score I kept until the end of the contest.
It seemed like a good idea, and it turned out it was. However, some other players went further, with varying scores depending on the deck you already had, and achieved even better results.
Playing phase
A key point here, since as I said earlier, it is impossible to simulate the game until a terminal state, is an evaluation function.
I used the same one for both the summoning and the attacking phase (you could even unsplit these two parts and evaluate them at the same time). During the contest, I built several functions:
Evaluation function 1 - Complex
The first I built (and the one I used in the end) is a function that takes the following form :
\[HP_{me} - HP_{opponent} + \displaystyle \sum_{\forall \; card \; \in \; B_{me}} f(card) - \displaystyle \sum_{\forall \; card \; \in \; B_{opponent}} f(card)\]where $B_{me}$ (respectively $B_{opponent}$) is my board (respectively the opponent’s board), and $f$ is an evaluation function for each card, that takes the following (complex form) :
public double f(int n,int mineHp,int opponentHp){
double score = 2*(double)this.defense + 5*(double)this.attack;
if (opponentHp <= this.hpChangeOpponent && n == 0){
score += 1000;
}
if (this.guard && mineHp < 20 && n == 0){
score += 1.5*(double)this.defense;
}
if (this.CardDraw > 0 && mineHp < 15 && n == 0){
score += 4;
}
if (this.breaktrough){
score += ((double)this.attack - 1.0)*0.9;
}
if (this.drain){
score += 0.7*(double)this.attack;
}
if (this.lethal){
score += 20.0 - (double)this.attack;
}
if (this.ward){
score += (double)this.attack;
score += 4;
}
if (this.ward && this.lethal){
score += 20.0 - (double)this.attack;
}
if (mineHp < 10 && this.guard && n == 0){
score += 3*(double)this.defense;
}
if (opponentHp < 10 && this.breaktrough && n == 0){
score += (double)this.attack;
}
if (opponentHp < 10 && this.drain && n == 1){
score += (double)this.attack;
}
return score;
}
Evaluation function 2 - Simple
However, I also tried (unsuccessfully) other evaluation function during the contest. A simpler one was talking the same shape as above, but where $f$ was the score of each card from the drafting phase.
Evaluation function 3 - Tempo
The last one was based on the tempo of the player. Here is a definition from an Hearthstone Wiki :
While tempo is often considered to be a common term and fairly simple to understand, it is also often considered to be among the more difficult things in Hearthstone to describe by definition rather than by examples or through a practice run. Many suggestions have been made for verbally describing this use of tempo, some of which are below:
- The momentum of the match. Probably the original definition and among many unofficially accepted “right” ones. However, its imprecision can lead to misunderstandings and odd interpretations causing confusion in discussion.
- The change of the board state in a given time (usually either a play or a turn, as in “a good/bad tempo play/turn”). What this definition has in its favor is its simplicity, but this very simplicity means that it does not cover all the uses of this term.
- The speed at which a player is reaching his/her win condition. An alternate interpretation of the original definition that is especially useful when discussing decks that don’t mainly win by gaining board control or that don’t aim at reaching that goal at the start of the game.
- The value of the effect on the board state divided by the mana used. The main upside of this definition is its being in the form of a mathematical formula because in the future it could be applied to calculations.
I tried to evaluate both my and the opponent’s tempo, but this wasn’t successful either. This evaluation was, in fact, pretty complex too, using both players boards and life.
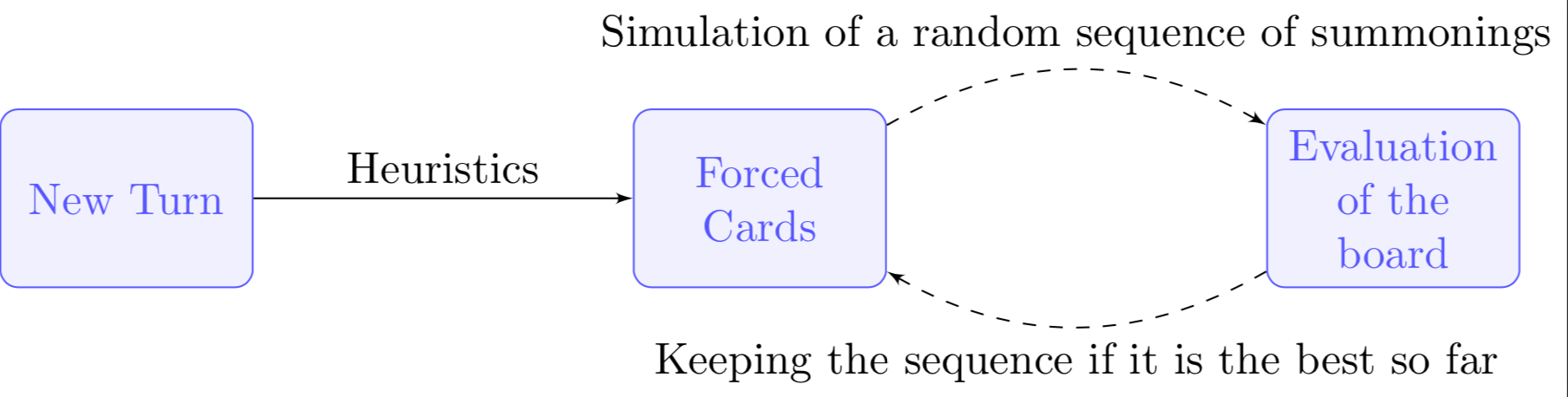
Summoning phase
The summoning phase was kept as simple as possible to waste as little time as possible.
First, I would check if I had to summon some cards. For example, a Guard card could save me if I was about to die, or a Charge card could finish the opponent immediately. Therefore, I would always check first if certain situations occurred and apply them directly.
Once this was done, I would generate a random sequence of possible cards to summon, simulate it, and evaluate the board. If the score was better than the current best, I would keep it.
Attacking phase
Regarding the attacking phase, my strategy was to implement a depth-3 MCTS, as shown in the figure below.
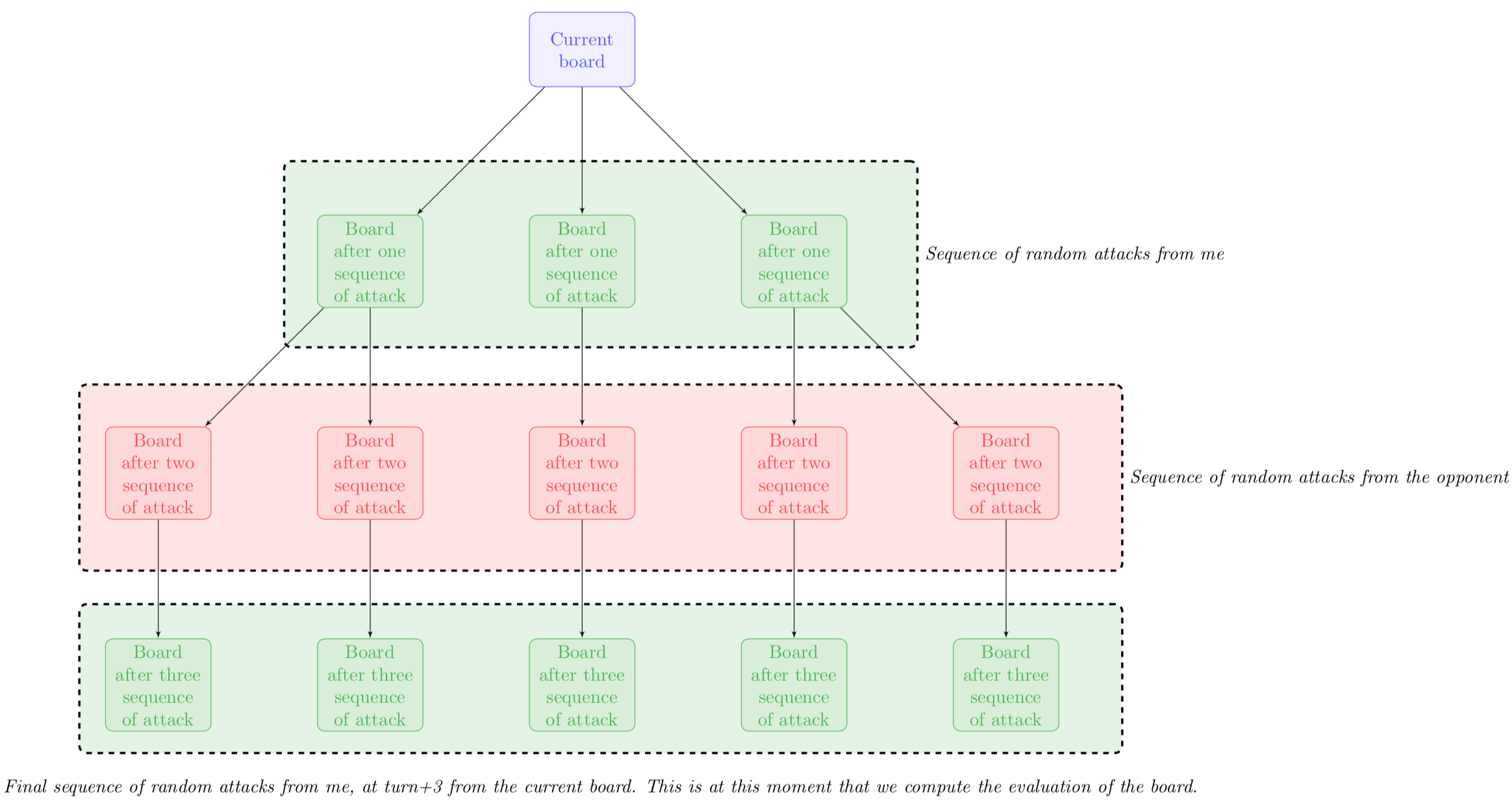
However, some minor changes had to be done. First, this scenario simulates attacks from the opponent and the MCTS selection has to be modified: you now have to take into account your loose (or your worst evaluation function) since you want the opponent to be as good as possible. Then, you can’t simulate the whole game until the end, and this is why I decided to stop the expansion phase at depth-3, with an evaluation of the board (rather than a boolean you win, you lose).
Finally, my code took the following form (with the time limit in mind):
| Actions | Allocated time |
|---|---|
| Sending outputs | 5ms |
| Response time for the summoning phase | 25ms |
| Response time for the attacking phase | 70ms |
Conclusion
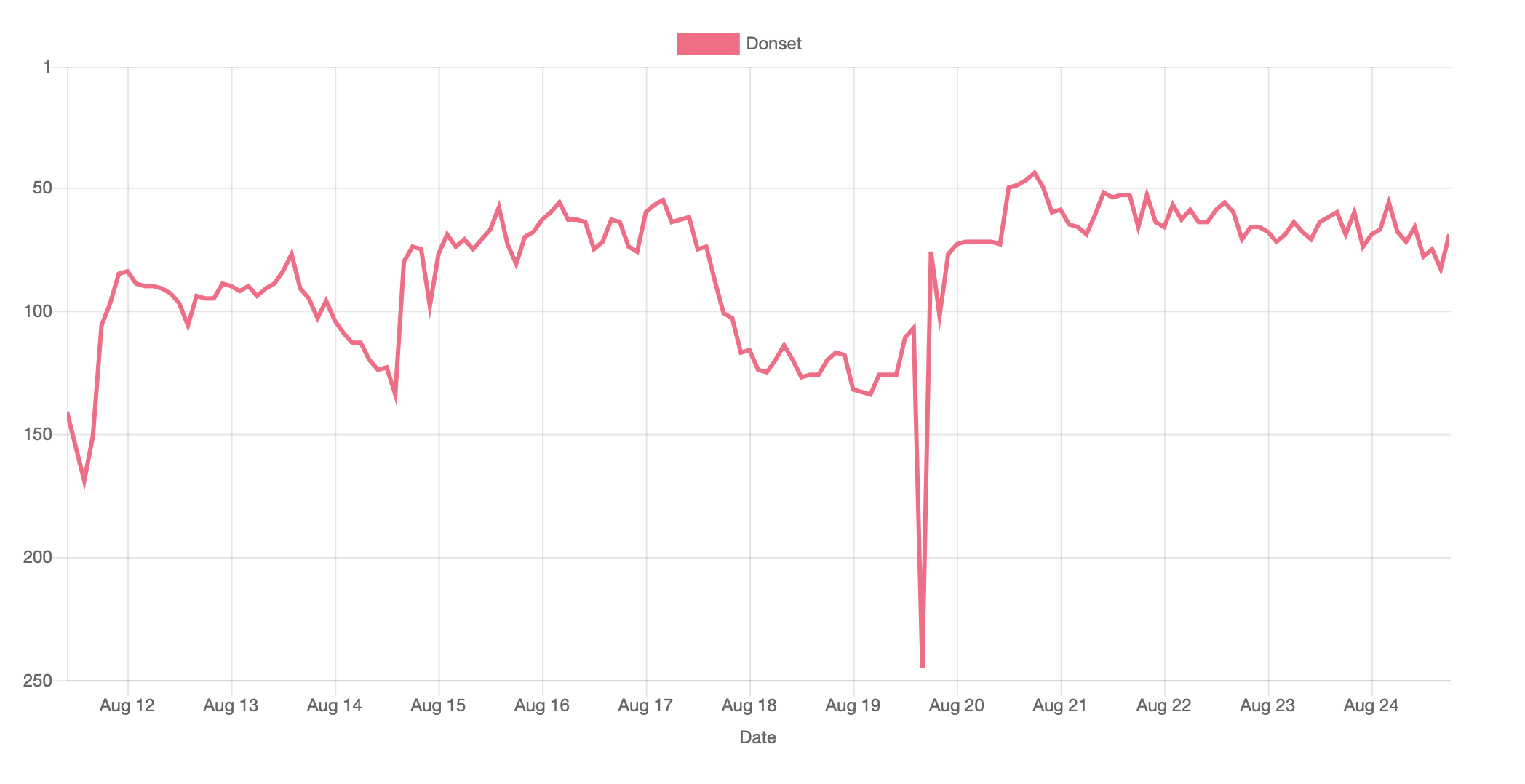
In the end, 2200 people participated in the contest. It was leagues based, and we were around 90 in the final league. To go to a higher league, you need to have a better score than the boss. The score is based on your wins and losses, against other players. You can find below my ranking throughout the contest. I ended up in the 69th position and the 11th best student.
Overall, it was an enjoyable contest. There was a lot of work to do, a lot of different aspects to take into account; several algorithms could be used: a great game!